#include <TRGNAlg.hh>
Inheritance diagram for RVLUmin::TRGNAlg< Scalar, Policy >:
Public Member Functions | |
| void | run () |
| int | getCount () const |
| convenience function for test codes | |
| TRGNAlg (Operator< Scalar > const &op, Vector< Scalar > &x, int _maxcount, atype _jtol, atype _agtol, atype _rgtol, atype _eta1, atype _eta2, atype _gamma1, atype _gamma2, atype _minstep, ostream &_str) | |
| constructor, first form. | |
| TRGNAlg (Operator< Scalar > const &op, Vector< Scalar > &x, Table &t, ostream &_str) | |
second form of constructor - passes most argument via a Table
| |
Approximates local solution of
![\[\min_x \|f(x)\|^2\]](form_42.png)
by a variant of the Steihaug-Toint trust region globalization of the Gauss-Newton algorithm, with flexible specification of the least-squares substep. See for instance T. Steihaug, "The conjugate gradient method and trust regions in large scale optimization", SIAM Journal on Numerical Analysis, v. 20 (1983), pp. 626-637; A. Conn, N. Gould, and P. Toint, Trust Region Methods, SIAM, 2000; and J. Nocedal and S. Wright, Numerical Optimization, Spring, 1999, esp. Ch 4.
Note that this algorithm will also approximate solutions of
![\[\min_x \|g(x)-b\|^2,\]](form_43.png)
provided that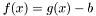 
is passed to the constructor.
The iteration updates the current solution estimate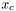 
to a new estimate 
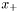by solving approximately the trust-region Gauss-Newton subproblem for the increment 
:
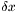![\[ \delta x = \mbox{argmin }\|Df(x_c)\delta x + f(x_c)\|^2 \mbox{ subject to } \|\delta x \| \le \Delta \]](form_48.png)
after which the update is computed as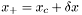 
.
The trust radius represents a size estimate of the region near 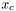in which the Gauss-Newton quadratic is a good approximation to the least-squares objective. The genius of the algorithm lies in the rules for updating 
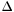: it is decreased by a factor < 1 when the actual decrease in the objective obtained by 
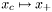is substantially less than the decrease predicted by the Gauss-Newton model, increased by a factor > 1 when the actual decrease is close to the predicted decrease and the trust region constraint is binding, and otherwise left alone. The step algorithm RVLUmin::TRGNStep manages 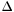- see its documentation for detailed information.
TRGNAlg depends on a choice of least squares solver with trust region truncation. This choice is passed by policy, that is, both by inheritance (mixin) and as a template parameter. The policy type must define a public member function with following signature:
[subtype of Algorithm and Terminator] * build(...) const;
with arguments
Policies should be default-instantiated, with no arguments, and should exhibit some sensible default behaviour (likely useless). For useful behaviour, some policies may require additional information - should be supplied in driver code by calling appropriate additional methods of particular policy classes.
The least squares solver built by the policy must be supplied with the attributes of both RVLAlg::Algorithm and RVLAlg::Terminator. The Algorithm::run() method changes the states of the arguments as described above. The Terminator::query() method returns true if trust region truncation was applied, else false (i.e. least squares solution approximation was interior to the trust region).
For example, the RVLUmin::CGNEPolicy class implements a policy as just described. Use it to specialize TRGNAlg to create a Gauss-Newton-Krylov or Steihaug-Toint algorithm, as described in the references mentioned earlier. The conjugate gradient iteration parameters must be supplied after instantiation for nontrivial execution, so the RVLUmin::CGNEPolicy includes a suitable method (assign(...)) whichh must be called on the TRGNAlg object after construction. See the TRGN functional test source for an explicit example of this use mode.
The step algorithm RVLUmin::TRGNStep manages both the solution of the least squares problem and the trust radius (data member Delta) - see documentation on RVLUmin::TRGNStep for details.
Parameters supplied to constructor. Absolute value type (eg. double for complex<double> denoted as abstype. See constructor docs for complete list:
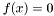, so any nontrivial "right-hand side" must be folded into the definition of 
.
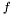). In some cases, it may be reasonable to stop when the objective gets small enough. To disable, set = zero. Typical value = 0.0
Usage: instantiate; call post-construction initialization of least-squares solver policy parent class if necessary to assign additional attributes; call RVLUmin::TRGNAlg::run().
Typical use case: see TRGN functional test source
Definition at line 469 of file TRGNAlg.hh.
| RVLUmin::TRGNAlg< Scalar, Policy >::TRGNAlg | ( | Operator< Scalar > const & | op, | |
| Vector< Scalar > & | x, | |||
| int | _maxcount, | |||
| atype | _jtol, | |||
| atype | _agtol, | |||
| atype | _rgtol, | |||
| atype | _eta1, | |||
| atype | _eta2, | |||
| atype | _gamma1, | |||
| atype | _gamma2, | |||
| atype | _minstep, | |||
| ostream & | _str | |||
| ) |
constructor, first form.
Parameters:
| op | - operator figuring in least-squares problem | |
| x | - solution Vector - initial guess on call, estimated solution on return | |
| _maxcount | - max permitted TR steps (calls to TRGNStep) | |
| _jtol | - stopping tolerance for least squares residual | |
| _agtol | - absolute stopping tolerance for gradient norm | |
| _rgtol | - relative stopping tolerance for gradient norm | |
| _eta1 | - lower G-A parameter | |
| _eta2 | - upper G-A parameter | |
| _gamma1 | - trust region reduction factor | |
| _gamma2 | - trust region expansion factor | |
| _initDelta | - initial trust radius | |
| _str | - verbose output stream |
Definition at line 550 of file TRGNAlg.hh.
| RVLUmin::TRGNAlg< Scalar, Policy >::TRGNAlg | ( | Operator< Scalar > const & | op, | |
| Vector< Scalar > & | x, | |||
| Table & | t, | |||
| ostream & | _str | |||
| ) |
second form of constructor - passes most argument via a Table
Definition at line 573 of file TRGNAlg.hh.
| void RVLUmin::TRGNAlg< Scalar, Policy >::run | ( | ) | [virtual] |
| int RVLUmin::TRGNAlg< Scalar, Policy >::getCount | ( | ) | const |
1.4.7