RVLUmin::PowerMethod< Scalar > Class Template Reference

Power method for finding largest singular value of a linear operator. More...

#include <pow.hh>

Inheritance diagram for RVLUmin::PowerMethod< Scalar >:


Public Member Functions
	PowerMethod (Vector< Scalar > &x, AScalar &sig, LinearOp< Scalar > const &A, int nstep, AScalar tol, ostream &str)
	Constructor parameters:.
void	run ()
int	getCount ()

Detailed Description

template<typename Scalar>
class RVLUmin::PowerMethod< Scalar >

Power method for finding largest singular value of a linear operator.

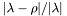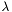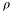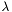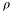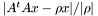Algorithm: stopping criterion based on an estimate of the relative residual $|\lambda - \rho|/|\lambda|$ , in which $\lambda$ is the largest eigenvalue of the normal operator and $\rho$ is the current Rayleigh quotient. Since $\lambda$ is not available, this numerator is approximated by the residual norm, the denominator by $\rho$ : thus the error estimator is $|A^tAx - \rho x|/|\rho|$ .

Parameters: The only two characteristic parameters required by this algorithm are the max number of steps permitted, and the stopping tolerance for the relative residual test. Reasonable values for these depend on the convergence rate, which is a function of the distribution of singular values. An isolated largest singular value (or group of singular values near the max) produces fastest convergence, with an elementary estimate showing dependence of the rate on the gap between largest and next-largest singular values (eg. Parlett, The Symmetric Eigenvalue Problem, SIAM, 1998). Thus, no general guidance may be given for selection of these parameters.

Other parameters supplied to the constructor are mutable references for the singular value and vector workspace, and a const reference for the operator. See constructor docs.

Typical use case: see functional test source.

Definition at line 181 of file pow.hh.

Constructor & Destructor Documentation

template<typename Scalar>

RVLUmin::PowerMethod< Scalar >::PowerMethod	(	Vector< Scalar > &	x,
		AScalar &	sig,
		LinearOp< Scalar > const &	A,
		int	nstep,
		AScalar	tol,
		ostream &	str
	)

Constructor parameters:.

Parameters:

	x	= initial singular vector estimate - mutable reference, updated on return
	sig	= initial singular value estimate - mutable reference, updated on return
	A	= linear operator for which singular pair is sought - const reference
	nstep	= number of power method iterations permitted. Typical value = 50.
	tol	= stopping threshold for error estimator. Typical value = 0.001
	str	= output stream on which to report progress of iteration