RVLUmin::ChebAlg

RVLUmin::ChebAlg< Scalar > Class Template Reference

Chebyshev polynomial algorithm - efficient implementation for normal equations

\[ A^{\prime} A x = A^{\prime} b\]

for solving the linear least squares problem

\[ \min_{x} \vert A x - b \vert^2 \]

. More...

#include <chebalg.hh>

Inheritance diagram for RVLUmin::ChebAlg< Scalar >:

RVLAlg::Algorithm List of all members.

Public Member Functions

 ChebAlg (RVL::Vector< Scalar > &_x, LinearOp< Scalar > const &_inA, Vector< Scalar > const &_rhs, atype &_rnorm, atype &_nrnorm, atype _gamma=0.04, atype _epsilon=0.001, atype _alpha=1.1, atype _lbd_est=0.0, int _maxcount=10, ostream &_str=cout)
 Constructor.
 ~ChebAlg ()
void run ()
int getCount () const
int getTotalCount () const
int getRestartCount () const
atype getSpectrumBound () const

Detailed Description

template<typename Scalar>
class RVLUmin::ChebAlg< Scalar >

Chebyshev polynomial algorithm - efficient implementation for normal equations

\[ A^{\prime} A x = A^{\prime} b\]

for solving the linear least squares problem

\[ \min_{x} \vert A x - b \vert^2 \]

.

This is Chebyshev iteration Algorithm as stated in Symes and Kern, Geophysical Prospecting vol. 42 pp. 565-614 1994 (see p. 578). We use variable names following Symes and Kern's notation insofar as possible.

Step 1:

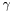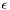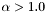Choose an inversion level $\gamma$, typically 0.04; Choose an error reduction factor $\epsilon$; Choose a 'fudge factor' $\alpha>1.0$.

Step 2: Compute the Chebyshev coefficients and estimate the necessary number of iterations.

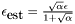$ \epsilon_{\mbox{est}}=\frac{\sqrt{\alpha}\epsilon} {1+\sqrt{\alpha}}$;

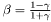$ \beta = \frac{1-\gamma}{1+\gamma}$;

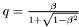$ q = \frac{\beta}{1+\sqrt{1-\beta^2}} $.

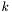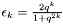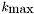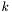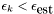Define error reduction factor after $k$ step as $ \epsilon_k=\frac{2q^k}{1+q^{2k}}$. Let $ k_{\mbox{max}} $ be the smallest $k$ which satisfies $ \epsilon_k< \epsilon_{\mbox{est}} $.

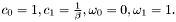
$ c_0 =1, c_1=\frac{1}{\beta},\omega_0=0,\omega_1=1. $

For 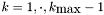$k=1,\cdot,k_{\mbox{max}}-1$, compute

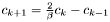$ c_{k+1} = \frac{2}{\beta}c_k-c_{k-1}$,

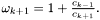
$ \omega_{k+1}=1+\frac{c_{k-1}}{c_{k+1}}.$

Step 3: Application of the Chebyshev polynomial by recursive application of the normal operator.

a. Initialization

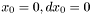$ x_0 = 0, dx_0 =0$,

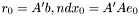$ r_0 = A^{\prime}b, ndx_0=A^{\prime}Ae_0$.

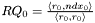$ RQ_0 = \frac{\langle r_0, ndx_0\rangle } {\langle r_0, r_0 \rangle} $.

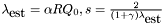$ \lambda_{\mbox{est}} = \alpha RQ_0, s = \frac{2}{(1+\gamma)\lambda_{\mbox{est}}}$.

b. Iteration

For 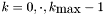$k=0,\cdot, k_{\mbox{max}}-1$

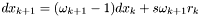$ dx_{k+1} = (\omega_{k+1}-1)dx_k+s\omega_{k+1}r_k$,

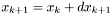$ x_{k+1} = x_k + dx_{k+1}$,

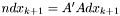$ ndx_{k+1} = A^{\prime}A dx_{k+1}$,

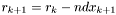$ r_{k+1} = r_k-ndx_{k+1}$,

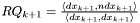$ RQ_{k+1}=\frac{\langle dx_{k+1},ndx_{k+1}\rangle} {\langle dx_{k+1},dx_{k+1}\rangle}$.

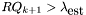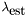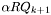if $ RQ_{k+1}> \lambda_{\mbox{est}}$, replace $\lambda_{\mbox{est}}$ by $\alpha RQ_{k+1}$. Recompute 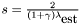$ s = \frac{2}{(1+\gamma)\lambda_{\mbox{est}}}$, and restart step b.

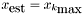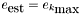The final outputs are the estimated solution $x_{\mbox{est}}=x_{k_{\mbox{max}}}$ and the estimated normal residual $e_{\mbox{est}}=e_{k_{\mbox{max}}}$.

Structure and function: Combines ChebStep with a Terminator which displays iteration count, residual norm, and normal residual norm on output stream (constructor argument _str), and terminates if iteration count exceeds max or residual norm or normal residual norm fall below threshhold (default = 10*sqrt(macheps)).

Usage: construct ChebAlg object by supplying appropriate arguments to constructor. On return from constructor, solution vector initialized to zero, residual norm to norm of RHS, and normal residual norm to norm of image of RHS under adjoint of operator. Then call run() method. Progress of iteration written on output unit. On return from run(), solution vector stores final estimate of solution, and residual norm and normal residual norm scalars have corresponding values.

Typical Use: see functional test source.

IMPORTANT NOTE: This class is also an RVLAlg::Terminator subclass.

IMPORTANT NOTE: The solution vector and residual and normal residual scalars are external objects, for which this algorithm stores mutable references. These objects are updated by constructing a ChebAlg object, and by calling its run() method.

IMPORTANT NOTE: this version of the algorithm initializes the solution vector to zero. To accommodate nontrivial initial guess, modify the right-hand-side vector (argument _rhs) externally.

IMPORTANT NOTE: in order that this algorithm function properly for complex scalar types, a careful distinction is maintained between the main template parameter (Scalar) type and its absolute value type. All of the scalars appearing in the algorithm are actually of the latter type.

See constructor documentation for description of parameters.

Definition at line 345 of file chebalg.hh.

Constructor & Destructor Documentation

template<typename Scalar>
RVLUmin::ChebAlg< Scalar >::ChebAlg ( RVL::Vector< Scalar > &  _x,
LinearOp< Scalar > const &  _inA,
Vector< Scalar > const &  _rhs,
atype &  _rnorm,
atype &  _nrnorm,
atype  _gamma = 0.04,
atype  _epsilon = 0.001,
atype  _alpha = 1.1,
atype  _lbd_est = 0.0,
int  _maxcount = 10,
ostream &  _str = cout 
)

Constructor.

Parameters:
_x - mutable reference to solution vector (external), initialized to zero vector on construction, estimated solution on return from ChebAlg::run().
_inA - const reference to LinearOp (external) defining problem
_rhs - const reference to RHS or target vector (external)
_rnorm - mutable reference to residual norm scalar (external), initialized to norm of RHS on construction, norm of estimated residual at solution on return from ChebAlg::run()
_nrnorm - mutable reference to normal residual (least squares gradient) norm scalar (external), initialized to morm of image of RHS under adjoint of problem LinearOp on construction, norm of estimated normal residual at solution on return from ChebAlg::run()
_gamma - inversion level for Chebyshev
_epsilon - stopping threshold for normal residual norm
_alpha - 'fudge factor'
_maxcount - max number of iterations permitted, default value = 10
default value = max absval scalar (which makes the trust region feature inactive)

Parameters:
_str - output stream

Definition at line 389 of file chebalg.hh.

template<typename Scalar>
RVLUmin::ChebAlg< Scalar >::~ChebAlg (  ) 

Definition at line 441 of file chebalg.hh.

Member Function Documentation

template<typename Scalar>
void RVLUmin::ChebAlg< Scalar >::run (  )  [virtual]

Implements RVLAlg::Algorithm.

Definition at line 443 of file chebalg.hh.

References RVLAlg::CountTerminator::getCount(), RVLAlg::VectorCountingThresholdIterationTable< Scalar >::init(), and RVLAlg::LoopAlg::run().

template<typename Scalar>
int RVLUmin::ChebAlg< Scalar >::getCount (  )  const

Definition at line 476 of file chebalg.hh.

template<typename Scalar>
int RVLUmin::ChebAlg< Scalar >::getTotalCount (  )  const

Definition at line 477 of file chebalg.hh.

template<typename Scalar>
int RVLUmin::ChebAlg< Scalar >::getRestartCount (  )  const

Definition at line 478 of file chebalg.hh.

template<typename Scalar>
atype RVLUmin::ChebAlg< Scalar >::getSpectrumBound (  )  const

Definition at line 479 of file chebalg.hh.

The documentation for this class was generated from the following file:
Generated on 5 Jan 2017 for RvlUmin by  doxygen 1.4.7